Division of Complex Numbers

The things missed in Mathematics!

1.       Here is the definition first:

2.       (a + ib)/(c + id) = ((ac  + bd)/(c² + d²)) + i((bc - ad)/( c² + d²))

3.       All the rules are the same as told in the addition and multiplication of the complex numbers.

4.       So, to let you remember the division formula, once again comes the Inverted Multiplier Man!

5.       Inverting the Multiplier Man has changed combining sign between the terms, they have got reversed (ac + bd) instead of (ac – bd) and (bc – ad) instead of (bc + ad).

6.       Also, inverting Multiplier Man also consumed some energy and hence the real and imaginary part got divided by the absolute value of the divisor (c + id).

·         To derive the above division formula, just multiply the numerator and denominator with the conjugate of the divisor (c + id), that is to say multiply by (c – id)

Multiplication of Complex Numbers

The things missed in Mathematics!

1.       First things first, the multiplication of two complex numbers is:

2.       (a + ib)x(c + id) = (ac – bd) +i(bc + ad)

3.       All the arguments applied to the addition of complex numbers applies to this as well, that is to say the absolute value and the argument of the result change in a complex manner (we will see how it can be simplified in further blogs).

4.       So, to simply help you to remember these formulas, here comes the Multiplier Man!

5.       Consider only the slanted lines in the face of Multiplier Man and the red line joining the extreme left and right lines ( a and d).

6.       The terms in the multiplication are simply made by the junctions of the slanted lines.

7.       And anything above the nose level in the face is combined by a minus sign and anything below nose level by the plus sign.

8.       And as usual, real and imaginary parts are combined by the plus sign.

Addition and Subtraction of Complex Numbers

The things missed in Mathematics!

1.       Addition of two complex numbers is very easy to do.

2.       Addition of two complex numbers (a + ib) and (c + id) is simply (a +c) + i(b + d).

3.       But do not consider it like simple algebra of real numbers. At a very subtle level it is different from the normal algebra.

4.       Consider this addition as filling up two containers of different shape as shown in the below figure.

5.       The left container shows the addition of real parts and the right container shows the addition of imaginary parts.

6.       Adding two complex numbers here is simulated by adding two different liquids (blue liquid and yellow liquid) in the containers.

7.       For this situation, the above representation of addition only tells you about the increase in weight of the two containers.

8.       But what about the rise in the level of the liquids? For the container representing the real part, it is straight forward to measure the increase in the level of liquids.

9.       What about the rise in the level of the liquids in the container for imaginary parts? Well, that will change in different situations and it all depends upon from where¹ and at what angle² the liquids were poured in the container.

10.   With respect to complex numbers, it means that there are quantities in case of complex numbers that change very differently even if the addition looks simple.

11.   These quantities are the ¹absolute value and the ²argument of the complex numbers.

Complex Conjugate

The things missed in Mathematics!

1.       There is a little strangeness in imagining things.

2.       With complex numbers, if a complex number satisfies an equation then there is another complex number also that will satisfy that equation and it is very similar to the first one.

3.       So, there is a pair of twin complex numbers that will satisfy the equation. They are called conjugate of each other.

4.       These two complex numbers are like the two faces of the same coin.

5.       You can buy only the thing that is worth of the value of the coin. (consider buying as satisfying an equation in the case of complex numbers)

6.       Now it is up to you that what you want to imagine, whether you have bought that thing using its head side or the tail side!

7.       The two sides individually also have the same value. Now what that value is in case of complex numbers?

8.       Consider a complex number a + ib, then its conjugate is a – ib, both the numbers have same absolute value defined as √(a² + b²). This is the value that remains same for the twin complex numbers.

Representations of Complex Numbers

The things missed in Mathematics!

1.       Complex numbers are more conveniently represented geometrically.

2.       Why geometrically? As you can see, to know a complex number you need to know two things – real part and imaginary part (a & b in a + ib).

3.       The basic object that you can draw that can be seen easily is a line (ideally you should not be able to distinguish between two points on a plane).

4.       To draw a line on a plane you require at least two information about it – two points through which it pass, its length and one end point or length and the angle that it makes with respect to an assumed reference line and so on.

5.       It is just like if you are travelling from a city A to some other city then you have to specify both how much distance you are covering (or how much time is it going to take) and in what direction you are travelling.

6.       If you don’t provide both the information, anyone can conclude anything and that most probably will be wrong!

7. So due to this property of Complex numbers, their geometric representation is suitable.

Argand Plane

1.       Consider the following setup

1.       In this diagram there is a huge mirror and a stick is kept on the ground with one end touching the surface of the mirror and is perpendicular to it.

2.       In this setup, the stick is the real object and the image is the imaginary part.

3.       An Argand Plane follows the same concept. The real stick is considered the x-axis and represents the real numbers.

4.       The mirror is considered y-axis and represents the imaginary part.

Polar Form

1.       Let us shoot an arrow with a rope attached to its end. The situation will look like the following picture.

1.       Here, the observable things are the rope and the arrow.

2.       Suppose you decided to know the position of the arrow as it will follow its trajectory in the air.

3.       But, can you locate those points by reaching at the arrow’s position? Let us see what you can measure by being standing at one position.

4.       First thing is the rope’s length as you will have it wounded around a wheel from which the rope will be pulled and by putting a measuring device at the point the rope is pulled, you will get its length.

5.       Second thing is the angle the rope makes at any time from the horizontal ground. That also can be measured by a device that measure angles (or it is possible to make such a device if one doesn’t exist).

6.       If you know these two things, and by using your trigonometry knowledge you can easily derive that rcosΘ and rsinΘ are the horizontal and vertical (a and b in a + ib) distance of any given point through which the arrow has passed.

7.       And hence the polar representation of the complex numbers is r(cosΘ + isinΘ).

8.       Also the give you the parlance with real and imaginary parts, consider two forces – the force you applied and the force of gravity.

9.       If you consider the force that you applied to be real, because you can measure that by yourself, this force is responsible for moving the arrow forward.

10.   The force that brings it down is the force of gravity, and you are not aware of that directly.

11.   You can suppose the force working along horizontal as purely real and the force of gravity as imaginary and the trajectory of the arrow is the effect of combination of both!

Complex Numbers

The things missed in Mathematics!

1.       Complex numbers are named as “complex” to sound it like that it is really something complex and out of this world but, this is not the case!

2.       Complex numbers are also developed on the same lines as the real numbers are invented.

3.       To explain how it is same, let us understand it in terms of the objects and its shadow.

4.       Suppose you have one light source and a stick fixed inside the ground.

5.       For different angles of the light source you will get the corresponding shadow of the stick on the ground.

6.       What will happen if you keep the light source exactly above the stick? Does the shadow of the stick cease to exist? No right?

7.       The real numbers are like the situations in which the shadows are observable directly (that’s why real numbers).

8.       And the complex numbers are like the shadow when the light source is exactly above the stick and is not directly observable and hence we have to “imagine” that it has a shadow.

Few formalized representations:

A complex number is represented as a + ib, where a, b are real numbers and i = √-1.

Origin of Complex numbers – Casus Irreducibilis

The things missed in Mathematics!

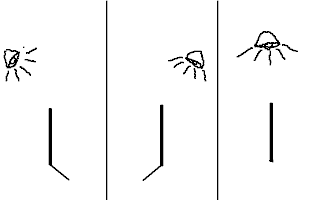
1.       Consider the following problem in the picture below

2.       In this problem you have to connect all the six circles with only two straight lines without lifting your pen from the paper.

3.       Seems simple! Try it out.

4.       Here is one way to do it – magnify the circles so that they become large circles. Apply this magical transformation and you will observe that you can easily do that as shown in the below picture. In this case the problem will be solved and also you don’t have to move outside the rectangle containing the circles (if you are under the impression that you don’t have to cross boundaries of the rectangle)

5.       But now, you have the question why and how this magical transformation came up? Well, the problem is actually well solved. If you can make your pen’s tip so thin that it can draw a very thin line and can draw straight lines at very minute angles, it is actually equivalent to magnifying the circles.

6.       Problem is, this solution is at very subtle level and difficult to prove its applicability if the distance between the two rows of circles is varied.

7.       To solve this problem in general terms you have to follow the following method by removing the restriction of moving within the rectangle containing the circles.

8.       Now the problem is solved in general terms, without modifying our problem statement and explaining too many things to solve this problem.

Parlance with Casus Irreducibilis

1.       The problem stated above is same as the problem of solving a cubic equation of the form

ax³ + bx² + cx + d = 0 where a, b, c and d are real numbers and x is a variable.

2.       First by applying Tschirnhaus transformation (yes, it is like magnifying the circles in our above problem), x = t – (b/3a); now keep wondering how this transformation came up out of nowhere!

3.       We will get another equation in t: t³ + pt + q = 0 where p = (3ac – b²)/3a² and q = (2b³ – 9abc + 27a²d)/27a³  . This form is also called Depressed cubic (This form doesn’t have squared part in it).

4.       If we solve the above equation, then we solve our original equation.

5.       The following steps will describe the Cardano’s method to solve the equation of above type in t.

6.       There can be two variables u and v such that u + v = t.

7.       We get an equation in u and v: u³ + v³ + (3uv+p)(u + v) + q = 0.

8.       Now Cardano put one more restriction of 3uv + p = 0 – again a very magical restriction, it would seem unfathomable to know its rationale!

9.       This gives us u³ + v³ = -q and u³v³ = -(p³/27). This means that v³ and u³ are the roots of the equation z² + qz –p³/27 = 0.

10.   By using quadratic formula to solve the above equation in z, we obtain

                         _____________                                   _____________

u³ = -(q/2) + √{(q²/4) + (p³/27)} and v³ = -(q/2) - √{(q²/4) + (p³/27)}

11.   Cardano didn’t know complex numbers and hence assumed the term √{(q²/4) + (p³/27)} to be real and ultimately derived the roots of the generic cubic.

12.   The final roots of the cubic can be real even if the square root term in the values for u³ and v³ is imaginary. That means even if you get the real roots, you can’t avoid making an intermediate calculation that will involve taking square root of negative numbers as the term (q²/4) + (p³/27) can be negative.

13.   The above situation where this term can be negative is called Casus Irreducibilis (the irreducible case).

14.   To avoid such a case the Complex numbers were invented. Also, invention of complex numbers explained the rationale of putting the restriction of 3uv + p = 0 by Cardano.

Logarithms

The things missed in Mathematics!

1.       You all must have observed this thing if you have tried to lift very heavy weights.

2.       If you want to lift the weight directly, it is not easy.

3.       But if you use a pulley as shown in the pic, the job is very much simpler.

4.       The concept of Logarithms in Mathematics is just the same.

5.       If you are doing a very lengthy calculation, which involves calculation of many powers of numbers, it is not so easy to do it directly.

6.       So, we can take another way to do it and use logarithms.

7.       What makes work easier with Logarithms? Answer is that it converts multiplication into addition and division into subtraction, both addition and subtraction being easier to perform than huge multiplications and divisions.

8.       Logarithms are also a way of asking the same question differently, that makes it easier to arrive at the answer.

9.       Instead of asking “What is a raised to power x?” Logarithms ask the question “If we have y that is a raised to power x, then what is x?

10.   Sometimes, asking the right question is more important in solving a problem, and Logarithms provide one of the ways to ask the right question.

Few formalized representations:

If y = a^x , then

x = log_ay

Mathematical Induction

The things missed in Mathematics!

1.       Let’s start a train travel. (Refer the pic below)

2.       You can always tell which station is after which one as you know in what sequence they will appear.

3.       The same thing is with Natural Numbers (Counting numbers), you know in what sequence the numbers should appear.

4.       And what is that define this sequence of numbers? In case with our train, it is the direction of the train in which it is travelling. In case of numbers, this train is the less than equal to relation (Yes the type of relation we saw during sets)!

5.       Now, suppose the train authorities perform some particular transactions at each station.

6.       You can consider these transactions as some formulas or rules on the natural numbers.

7.       How can you, with surety know about what these transactions are?

8.        If you see those transactions at any one of the stations, you are not sure if it was carried at that particular station only or on all the stations.

9.       To establish that those transactions are performed on every station, you need to see those transactions at different stations. But you can’t see them on all the stations!

10.   First thing to establish this rule is to see whether those transactions are performed at the starting station (Station 1).

11.   If you don’t see those transactions at the starting station itself, you know that the transactions are not standard rules.

12.   If you find that those transactions are performed at the starting station, then you should randomly select any station on the train’s route and see if those transactions are performed there. Suppose you find that those transactions are indeed performed there as well.

13.   But, you can’t travel faster than the train to reach the next station to see by yourself if the same transactions are performed on the next station as well.

14.   By the time you reach the next station, you see the train has already gone. But, you can still look out for the effects those transactions may have left at the next station.

15.   If you can find sufficient proof that logically can conclude that those transactions have been performed on the next station as well and you know that these proofs can be found on all the stations (may be because of law or any other rules by government).

16.   So, you will certainly know that these transactions are performed at all the stations and you can establish that as a fact!

17.   This is how Mathematical Induction works!

18.   This simple story has a tricky part as well. You can very well see that there is different information that you need to know at different times.

19.   First you should know the starting station. (This indicates, you should know from which number the particular formula starts applying to natural numbers)

20.   You should be well versed with the schedule of the train. (This amounts to have a deep knowledge about the counting of numbers itself, the less than equal to relation on numbers, etc. etc…)

21.   You should know the effects of operations, properties of operations on natural numbers, what are other relationships that exist with numbers using these operations (amount to knowing about the laws and rules made by the government).

22.   This is the philosophy of Mathematical Induction in Mathematics!

Binary Operations

The things missed in Mathematics!

1.       I like to travel a lot.

2.       See the map of Bangalore city below (Courtesy: Google Maps).

3.       You can see an intersection of roads circled.

4.       If you are coming from North to South, then this junction is simply a Binary Operation.

5.       The two roads belong to Bangalore City Roads (a Set).

6.       And these two roads combine to give another road that also belong to Bangalore City Roads.

Few formalized representations:

A binary operation on a set A is defined as a function from AxA to A. That is to mean, if you take any two elements from A and apply the binary operation, you will get another element from A.

For example, addition (+) on set of Natural numbers* is a binary operation (addition of two natural numbers gives us another natural number).

But, subtraction (-) on set of Natural numbers is not a binary operation (subtraction of two numbers can be negative, and negative numbers are not Natural numbers.

*Natural numbers are counting numbers, starting from 1,2,3,4,…

Composition of Functions

The things missed in Mathematics!

1.       Here is a process that is very familiar in our day to day life.

2.       It is the process of conversion of same water into ice or vapours.

3.       Here Heating, Refrigeration and Condensation are three different functions. Let us see how these are functions first of all.

4.       Heating changes the water from sets of liquids (water) to sets of gases (vapours) AND Ice to water (sets of solids to sets of liquids) and not vice versa. Hence a function.

5.       Refrigeration changes the water to ice (sets of liquid to sets of gases) and not vice versa. Hence a function.

6.       Condensation changes water vapours to liquid water and not vice versa. Hence a function

7.       Now what will happen if we apply these functions one after another? For example, Lets apply Heating on Ice followed by Heating of water. We get vapours from ice.

8.       Apply Heating of water followed by Condensation. We get water back again.

9.       All these examples are Composition of Functions.

10.   Also note that, the sequence in which these functions are applied does make a difference.

11.   All the sequences may not make sense (e.g. Refrigeration of water and then Condensation).

12.   All the valid sequences may not have an inverse sequence (e.g. Condensation of vapours and then Refrigeration gives us Ice, but Refrigeration of Ice and then Condensation of water is meaningless).

Few formalized representations:

A composition of two functions f and g on a variable x is represented by fog(x) or f(g(x)) and means that first the function g is applied on x and then the function f is applied on the result of g(x).