1. Complex numbers are more conveniently represented geometrically.
2. Why geometrically? As you can see, to know a complex number you need to know two things – real part and imaginary part (a & b in a + ib).
3. The basic object that you can draw that can be seen easily is a line (ideally you should not be able to distinguish between two points on a plane).
4. To draw a line on a plane you require at least two information about it – two points through which it pass, its length and one end point or length and the angle that it makes with respect to an assumed reference line and so on.
5. It is just like if you are travelling from a city A to some other city then you have to specify both how much distance you are covering (or how much time is it going to take) and in what direction you are travelling.
6. If you don’t provide both the information, anyone can conclude anything and that most probably will be wrong!
7. So due to this property of Complex numbers, their geometric representation is suitable.
Argand Plane
1. Consider the following setup
1. In this diagram there is a huge mirror and a stick is kept on the ground with one end touching the surface of the mirror and is perpendicular to it.
2. In this setup, the stick is the real object and the image is the imaginary part.
3. An Argand Plane follows the same concept. The real stick is considered the x-axis and represents the real numbers.
4. The mirror is considered y-axis and represents the imaginary part.
Polar Form
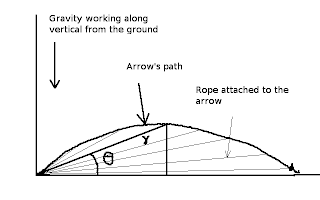
1. Let us shoot an arrow with a rope attached to its end. The situation will look like the following picture.
1. Here, the observable things are the rope and the arrow.
2. Suppose you decided to know the position of the arrow as it will follow its trajectory in the air.
3. But, can you locate those points by reaching at the arrow’s position? Let us see what you can measure by being standing at one position.
4. First thing is the rope’s length as you will have it wounded around a wheel from which the rope will be pulled and by putting a measuring device at the point the rope is pulled, you will get its length.
5. Second thing is the angle the rope makes at any time from the horizontal ground. That also can be measured by a device that measure angles (or it is possible to make such a device if one doesn’t exist).
6. If you know these two things, and by using your trigonometry knowledge you can easily derive that rcosΘ and rsinΘ are the horizontal and vertical (a and b in a + ib) distance of any given point through which the arrow has passed.
7. And hence the polar representation of the complex numbers is r(cosΘ + isinΘ).
8. Also the give you the parlance with real and imaginary parts, consider two forces – the force you applied and the force of gravity.
9. If you consider the force that you applied to be real, because you can measure that by yourself, this force is responsible for moving the arrow forward.
10. The force that brings it down is the force of gravity, and you are not aware of that directly.
11. You can suppose the force working along horizontal as purely real and the force of gravity as imaginary and the trajectory of the arrow is the effect of combination of both!



No comments:
Post a Comment